Lecture #7: ZOPA
なんだかBATNAやらZOPAやら、ウルトラマンに出てくる星人のような略語が続きますが、ご勘弁のほど。こういう略語が交渉学の世界では出回ってしまっているもので・・・。
今回のZOPAは Zone Of Possible Agreement の頭文字を取った略語です。そのまま訳すと、「合意可能領域」となります。
まずすごい単純な例を考えてみます。Aさん(売り手)、Bさん(買い手)2名はこれから、ある商品の売買価格について交渉をするところです。この2名には何の人間関係もなく、Aさんは安い価格、Bさんは高い価格を設定したいと思っています。そのほかに何の利害関心もありません。
ここで、AさんのBATNAは4,000円、BさんのBATNAは6,000円だとします。BANTAのことをよく思い起こしてほしいのですが、将来の人間関係などをとりあえず無視すれば、BATNAより悪い条件を受け入れることはありえません。よって、Aさんは4,000円以下の値段ならBさんには売りませんし、Bさんは6,000円以上の値段だとAさんからこの商品を買うことはありません。
これをグラフにしてみましょう。

このような状況では、Aさん、Bさんには交渉をする意味があります。つまり、4,000円から6,000円の間で交渉が妥結すれば、お互いにBATNAよりもよい交渉結果を得られるのです。
このとき、4,000円から6,000円の間の空間のことをZOPAと言います。また、ZOPAが存在するので交渉が合意に達しうる、という言い方もします。
ZOPAが広ければ広いほど、交渉は合意に達する可能性が高まります。しかし、BATNAの回で述べたとおり、交渉人はお互い自分のBATNAを改善しようとしますので、上記のような場合だと、次第に狭まってしまいます。
もし、AさんのBATNAが7,000円だとZOPAが存在しないので交渉は合意に達することができません。もし万が一、Aさんが妥協して6,000円で合意に達したとしたら、それはAさんの過ちで、Aさんは1,000円損をしたことになります。
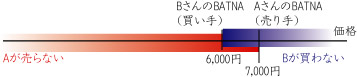
上の事例のように、取引するイシューが「価格」の一つに限定されていると、上の図のように直線上にZOPAを図示できますが、もし2つ以上あった場合はどうやって図示するのでしょう? 一般的に下の図のように図示されます。
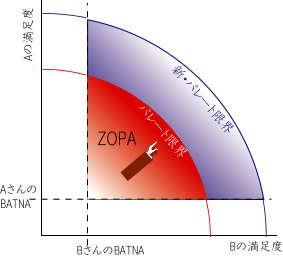
x軸、y軸にそれぞれの「満足度」をとって、BATNAがもたらす満足度を直線で表現します。イシューが2つ以上あるので、BATNAも複数のイシューそれぞれに条件がついているため、各条件を一つの尺度「満足度」にまとめて表現せざるを得ません。
ZOPAはどこにあるかと言うと、BATNAより右上、となります(一つ目の条件)。しかし交渉の取引物件には限界がある、つまり交渉で相手に差し出す手持ちのお金や資源には限りがあるので「パレート限界(最適)」という限界を示す曲線が描かれます(二つ目の条件)。よって、BATNAの直線、パレート限界で囲まれたエリアがZOPAとなります。
(パレート限界(最適)は交渉学講座4を参照)
交渉の取引材料が増えれば、つまり統合的交渉の回で説明したように、交渉を通じて自分と相手が異なる価値づけをしている事柄を見つけられれば、パレート限界は拡大され、結果としてZOPAは大きくなります。
ZOPAのエリアの中で、合意が見つかるわけですが、合意条件を図中の点として描いたときに、「右上」のほうにあればあるほど、お互いに満足がいく条件です。「左上」に進めばAが得してBが損をする、「右下」ならその逆ですが、「右上」ならお互い満足度がアップするので両者ともに文句はないでしょう。そうしてZOPAの中で右上に進んでいくうちにパレート限界に達するような合意条件を見つけられれば、お互いにとって最大ハッピーな合意に達した(イシューを増やさない限りそれ以上合意条件を改善しようがない状態に至った)ことになります。この状態をoptimalityなどと言います。
交渉学では「できる限り右上に進むこと」を強調しており、よく「北東に進む (go northwest)」と言います。もしパレート限界まで達しないところで合意してしまったら、それは「旅の途中」で面倒だから交渉を止めたことになり、suboptimalな状態、不十分な状態になります。私の師匠のL. Susskindはよく、super-optimalityと言って、単にoptimalな合意を追い求めるだけではなく、パレート限界を拡げることの重要性を語っています。
今回は少し難しい話をしましたが、これが交渉学における意思決定分析(decision analysis)の基礎です。ZOPAとパレート限界の話がおおむね理解できたら、交渉を「合理的に」分析する枠組みの基礎が理解できたと言えるでしょう。
以下に参考文献を挙げておきます。
